题目描述

输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树：

递归方法

这道题要充分用到二叉树前序遍历与中序遍历的数量关系.

示例中两个数组的关系进行分析可知:

前序遍历特点： 节点按照 [ 根节点 | 左子树 | 右子树 ] 排序，以题目示例为例：[ 3 | 9 | 20 15 7 ]

中序遍历特点： 节点按照 [ 左子树 | 根节点 | 右子树 ] 排序，以题目示例为例：[ 9 | 3 | 15 20 7 ]

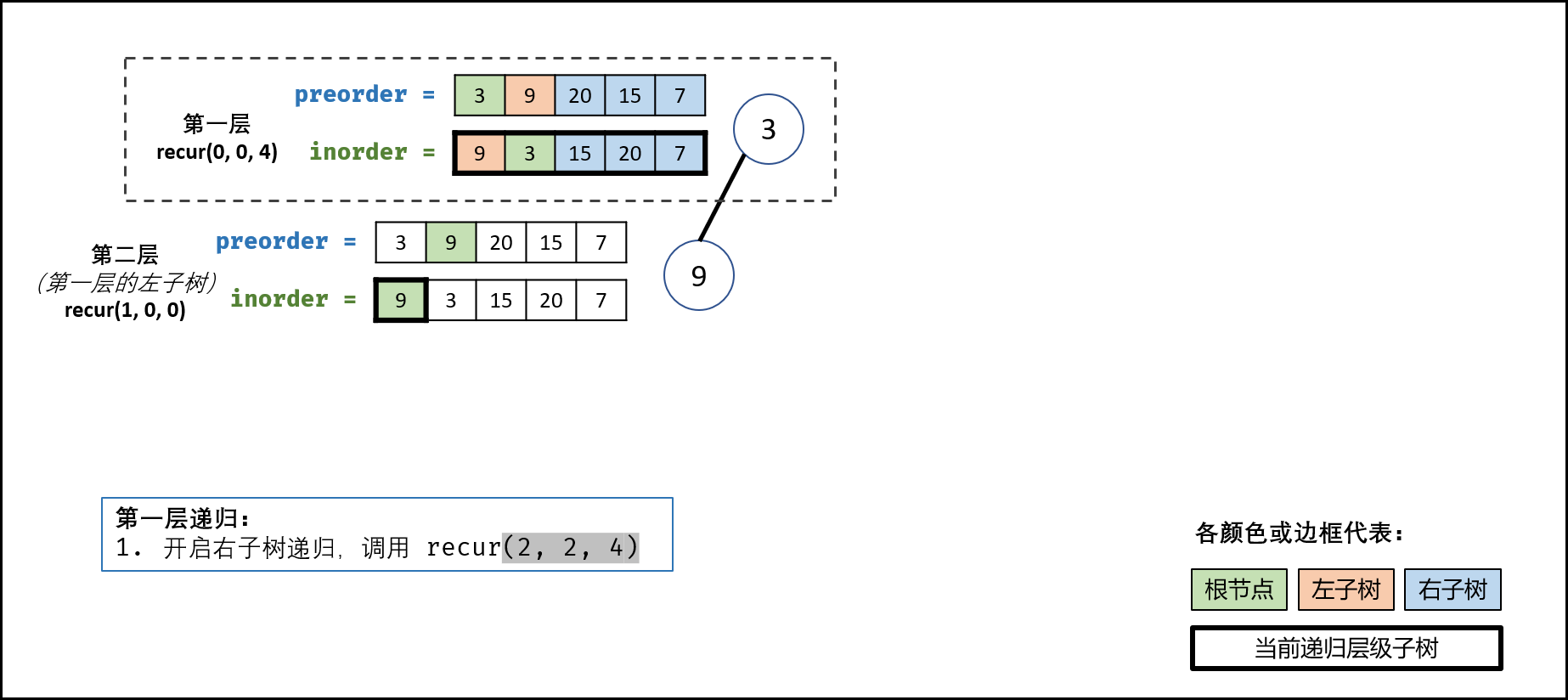
对于根节点3 来说, 它排在前序遍历数组的最前面, 在中序遍历数组中找到3 的位置, 可以发现在它之前的元素全部属于左子树, 在它之后的元素全部属于右子树.

这个这个规律可以套用到所有子树中, 比如20 是右子树的根节点, 它在前序遍历数组中位于该子树范围中的第一位([20, 15, 7]是右子树), 在中序遍历中找到20 的位置, 在其范围内([15, 20, 7]) 左边的元素都属于新的左子树, 右边的元素都属于新的右子树. 这样就构成了递归关系.

所以我们的递归思路是:

递归参数: 前序遍历中根节点的索引pre_root、中序遍历左边界in_left、中序遍历右边界in_right
终止条件： 当 in_left > in_right ，子树中序遍历为空，说明已经越过叶子节点，此时返回 null
递推工作：
1. 建立根节点root：值为前序遍历中索引为pre_root的节点值。
2. 搜索根节点root在中序遍历的索引i： 为了提升搜索效率，本题解使用哈希表 dic 预存储中序遍历的值与索引的映射关系，每次搜索的时间复杂度为 O(1)
3. 构建根节点root的左子树和右子树： 通过调用recur() 方法开启下一层递归。
  - 左子树：根节点索引为pre_root + 1 ，中序遍历的左右边界分别为 in_left 和i - 1。
  - 右子树：根节点索引为i - in_left + pre_root + 1（即：根节点索引 + 左子树长度 + 1），中序遍历的左右边界分别为i + 1和in_right。

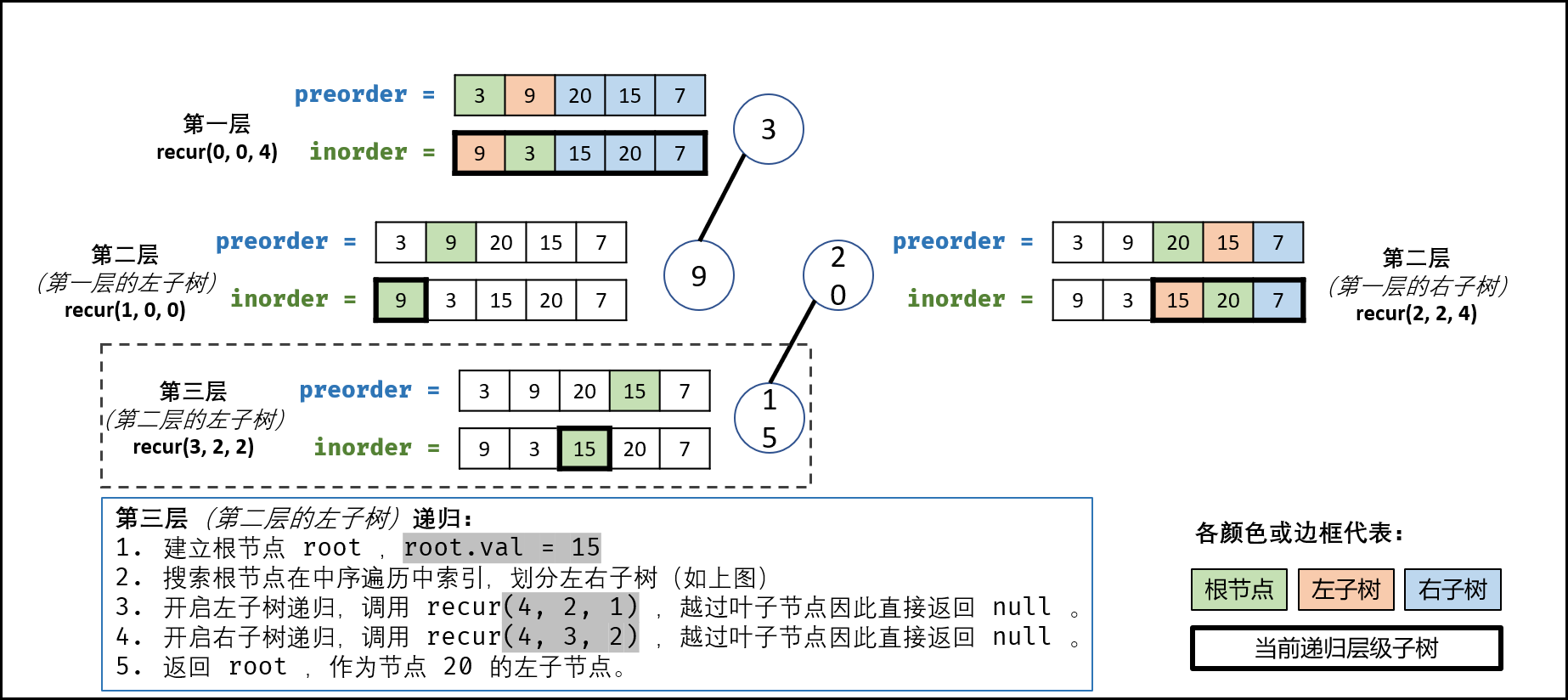
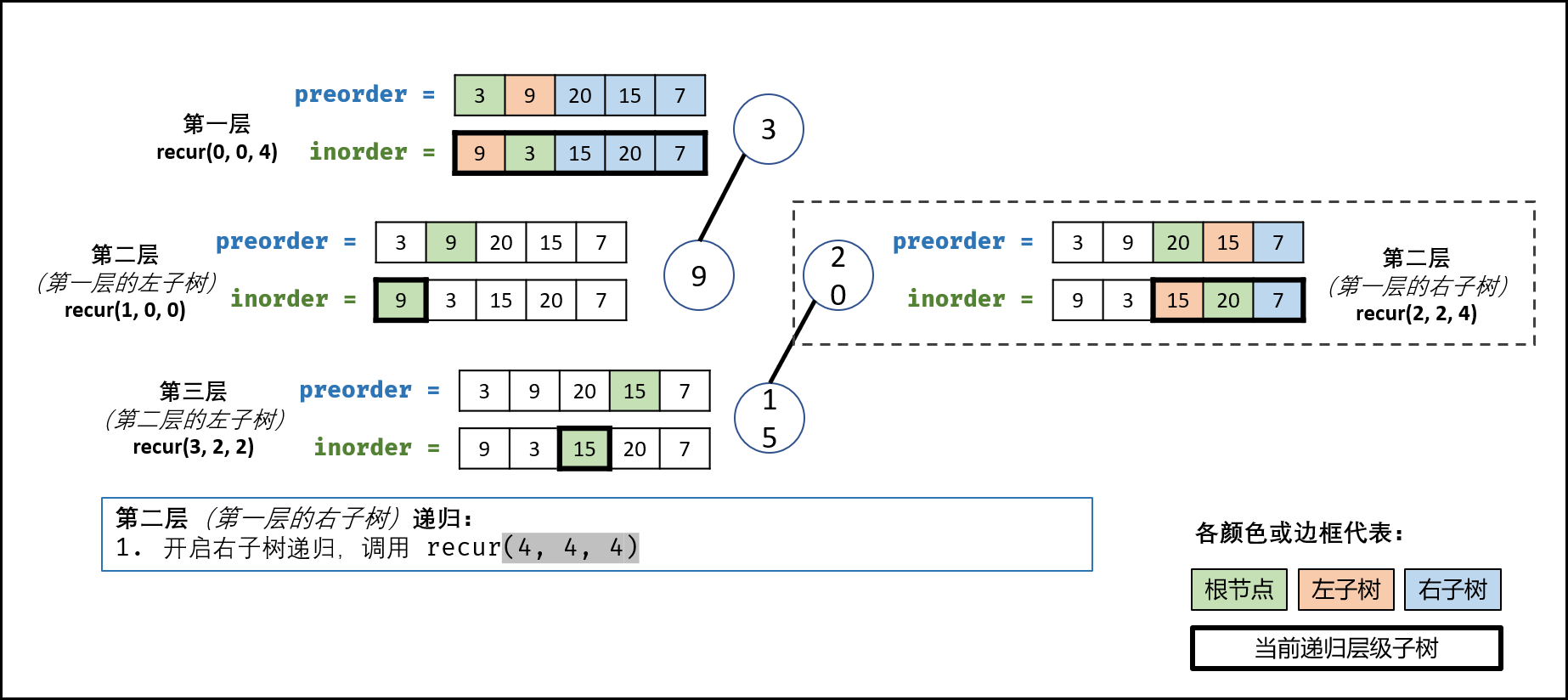
判断下一次递归时子树的左右边界比较容易, 就是当前i 值加一或减一即可, 判断左右子树的根节点时, 左子树根节点很容易, 当前节点在前序遍历数组中的后一个元素就是左子树的根节点. 下面来分析右子树根节点如何表示:

我们已经知道当前树的根节点在前序遍历数组中的索引pre_root , 它后面紧跟着的是左子树, 所以得出左子树节点的数量就可以得到右子树根节点的索引了.我们还知道当前树根节点在中序遍历数组中的索引i, 以及左子树的边界in_left ,那么i - in_left 就是左子树的节点数量. 所以右子树的根节点索引为i- in_left + pre_root + 1.

)

public class jz07 {
    private int[] pre;
    HashMap<Integer, Integer> dic = new HashMap<>();

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        pre = preorder;
        for (int i = 0; i < inorder.length; i++) {
            dic.put(inorder[i], i);
        }

        return recur(0, 0, preorder.length - 1);

    }

    private TreeNode recur(int pre_root, int in_left, int in_right) {
        if (in_left > in_right)
            return null;

        int i = dic.get(pre[pre_root]);
        TreeNode root = new TreeNode(pre[pre_root]);

        root.left = recur(pre_root + 1, in_left, i - 1);
        root.right = recur(i - in_left + pre_root + 1, i + 1, in_right);

        return root;
    }
}