jz55-Ⅱ.平衡二叉树

题目描述

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

示例一：给定二叉树 [3,9,20,null,null,15,7]

  3
 / \
9  20
  /  \
 15   7

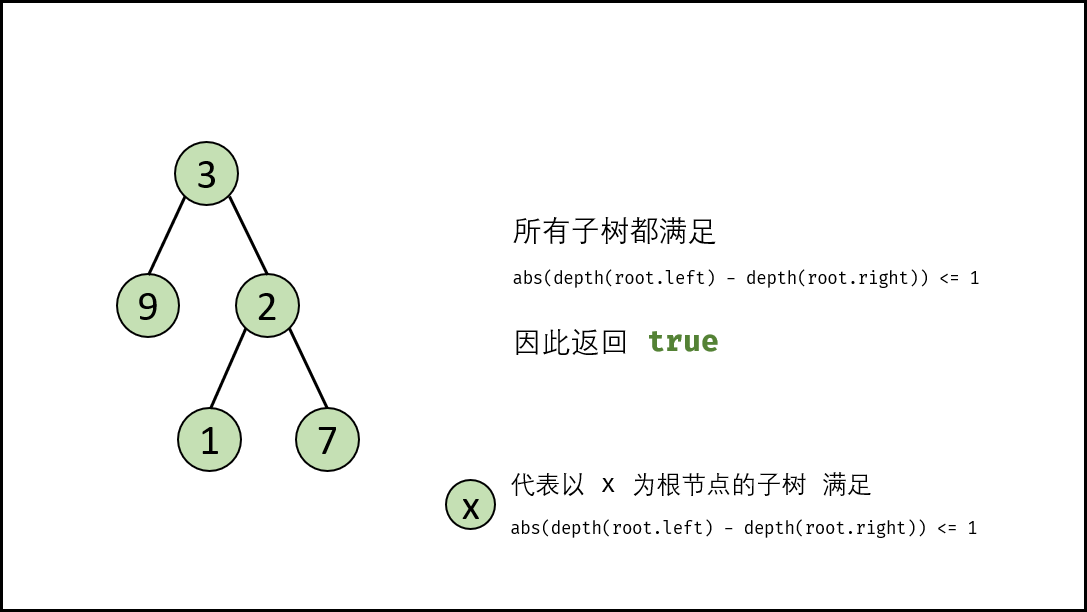
返回 true 。

示例二：给定二叉树 [1,2,2,3,3,null,null,4,4]

      1
     / \
    2   2
   / \
  3   3
 / \
4   4

返回 false 。

---

题解

先序遍历 + 判断深度(自顶向下)

根据上道题(jz55-Ⅰ)算出的树的深度进行拓展, 我们通过递归的方法已经算出了每个子树的深度, 假设用depth(root) 表示, 那么再嵌套一个递归:

isBalance(root):

1. *特例处理: * 如果root == null , 直接返回true ;

2. *递归过程: * 判断三个内容:

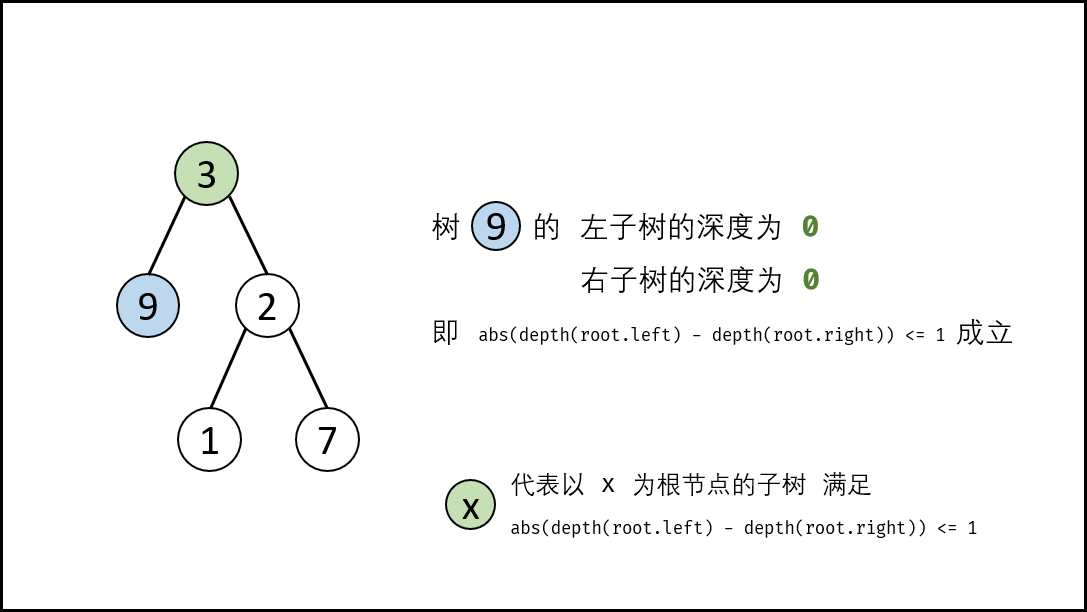
   1. 当前左右子树的差值是否小于等于1: Math.abs(depth(root.left) - depth(root.right)) <= 1
   2. 左子树是否为平衡树: isBalance(root.left)
   3. 右子树是否为平衡树: isBalance(root.right)

3. *返回值: * 将递归过程求出的三个内容用 && 连接起来, 返回值类型为 boolean

public boolean isBalanced(TreeNode root) {
    if (root == null)
        return true;
    return Math.abs(depth(root.left) - depth(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
}

private int depth(TreeNode root) {
    if (root == null)
        return 0;
    return Math.max(depth(root.left), depth(root.right)) + 1;
}

---

后序遍历 + 剪枝(从底至顶)

思路是对二叉树做后序遍历，从底至顶返回子树深度，若判定某子树不是平衡树则 “剪枝” ，直接向上返回。

算法流程：

recur(root) 函数：

• 返回值：

  1. 当节点root 左 / 右子树的深度差 ≤1 ：则返回当前子树的深度，即节点 root 的左 / 右子树的深度最大值 +1 （ max(left, right) + 1 ）；
  2. 当节点root 左 / 右子树的深度差 > 2：则返回 -1, 代表 此子树不是平衡树

• 终止条件：

  1. 当 root 为空：说明越过叶节点，因此返回高度 0；
  2. 当左（右）子树深度为 -1：代表此树的 左（右）子树 不是平衡树，因此剪枝，直接返回 -1 ；

public boolean isBalanced(TreeNode root) {
    return recur(root) != -1;
}

private int recur(TreeNode root) {

    if (root == null)
        return 0;
    int left = recur(root.left);
    if (left == -1) return -1;
    int right = recur(root.right);
    if (right == -1) return -1;

    return Math.abs(left - right) < 2 ? Math.max(left, right) : -1;

}