题目描述

给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

示例:

输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

题解

动态规划

这道题需要动手推导, 根据下图的关系:

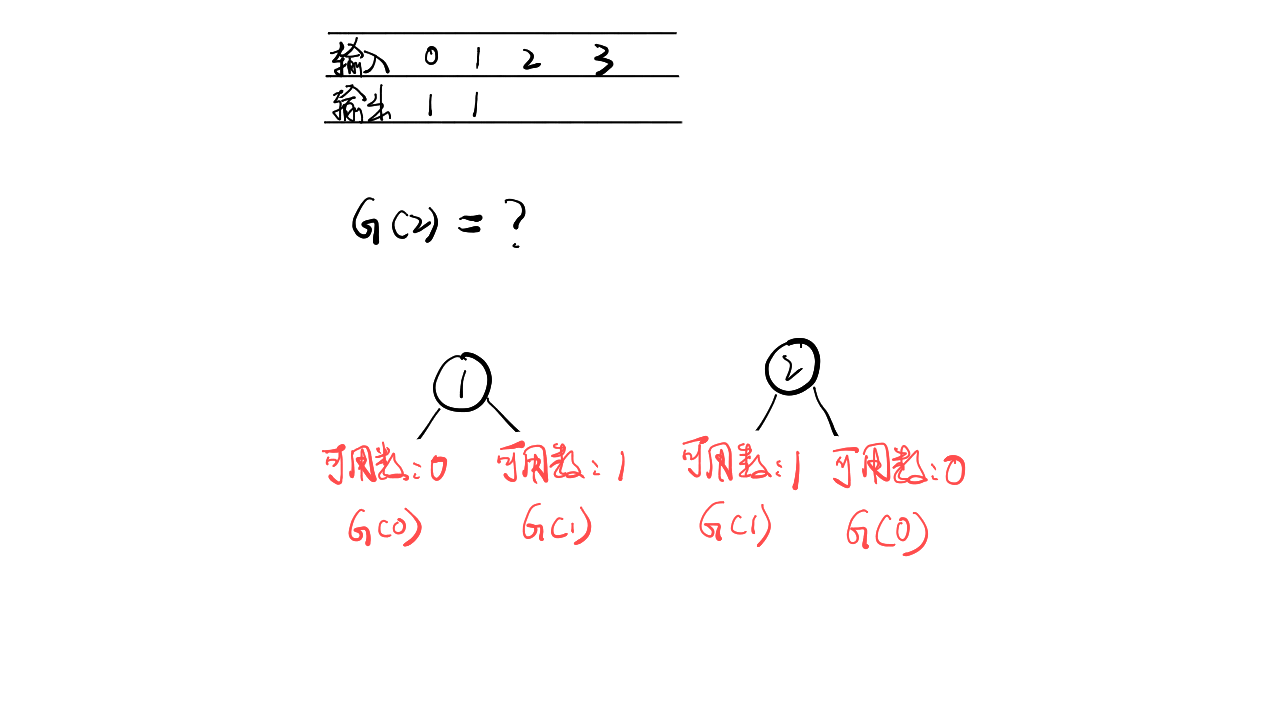
可以总结出思路, 对于n 个节点来说, 每个节点都可以作为根节点, 每个节点作为根节点的所有情况加起来就是n 个节点的总数量. 比如图中的 n=3 的情况, 就是节点1作为根节点的情况 + 节点2作为根节点的情况 + 节点3作为根节点的情况. 而每个节点作为根节点时的可能性数量又等于左右子树的情况相乘. 这就是一个动态规划的问题, 因为每个状态都与前几个状态有关.

G(n)=f(1)+f(2)+f(3)+f(4)+…+f(n)

其中

f(i)=G(i−1)∗G(n−i)

综合两个公式可以得到 卡特兰数公式

G(n) = G(0)G(n-1)+G(1)(n-2)+…+G(n-1)G(0)G(n)=G(0)G(n−1)+G(1)G(n−2)+…+G(n−1)G(0)

public class lc96 {
    public int numTrees(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;

        for (int i = 2; i < n + 1; i++) {
            for (int j = 1; j < i + 1; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }

        return dp[n];
    }
}