题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例：
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

题解

按列遍历求取

思路是逐个求出每一列能接多少单位水，加起来即可。
这里只要知道一个数量关系：
每遍历到一个列，要求出该列左边最高的列和右边最高的列，根据这三列的高度可以求出当前列能接多少雨水。
例如：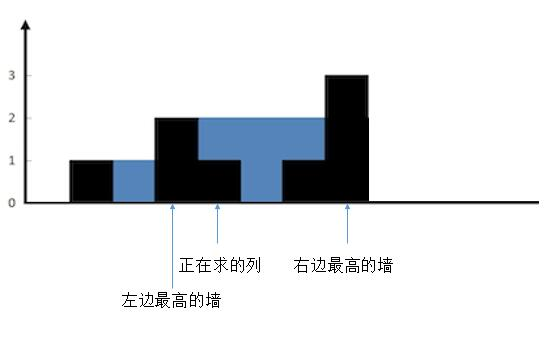

当前列高度为1,左边最高列高度为2,右边最高列高度为3,那么当前列能接的水数量就是左右两边较低列的高度与当前列高度的差值.具体流程为:

遍历到第i列时,分别求出左边最高列的高度maxL和右边最高列的高度maxR
求出maxL和maxR中较小的值为min
若min值小于等于i列的高度,当前列不接水.若min值大于i列高度,则能接min-height[i]单位的水

public int trap(int[] height) {
    int len = height.length;
    int ans = 0;
    for (int i = 1; i < len; i++) {
        int[] temp = maxSide(i, height);
        int min = Math.min(temp[0], temp[1]);
        if (height[i] < min) {
            ans += (min - height[i]);
        }
    }
    return ans;
}

private int[] maxSide(int index, int[] height) {
    int[] res = new int[2];
    int maxL = 0;
    int maxR = 0;
    for (int i = 0; i < index; i++) {
        maxL = Math.max(maxL, height[i]);
    }
    for (int i = index + 1; i < height.length; i++) {
        maxR = Math.max(maxR, height[i]);
    }
    res[0] = maxL;
    res[1] = maxR;
    return res;
}

动态规划

思路跟上面的解法一样,只不过上面的解法中每遍历一列都要重新遍历求出左右两边的最高高度,利用动态规划的方法可以简化过程.
分别使用数组maxL[i]和maxR[i]记录第i列的左右最高高度.有以下状态转移方程:
maxL[i]=max(maxL[i-1], height[i-1])
maxR[i]=max(maxR[i+1], height[i+1])

public int trap2(int[] height) {
    int res = 0;
    int[] maxL = new int[height.length];
    int[] maxR = new int[height.length];

    for (int i = 1; i < height.length; i++) {
        maxL[i] = Math.max(maxL[i-1], height[i-1]);
    }
    for (int j = height.length-2;j>=0;j--){
        maxR[j] = Math.max(maxR[j+1], height[j+1]);
    }

    for (int i = 1; i < height.length; i++) {
        int min = Math.min(maxL[i], maxR[i]);
        if (height[i] < min) {
            res += (min - height[i]);
        }
    }
    return res;
}

双指针

public int trap(int[] height) {
    int n = height.length;
    if (n < 3) {
        return 0;
    }

    int res = 0;
    int leftMax = height[0];
    int rightMax = height[n - 1];

    int l = 1;
    int r = n - 2;

    while (l <= r) {
        if (leftMax < rightMax) {
            res += leftMax > height[l] ? leftMax - height[l] : 0;
            leftMax = Math.max(leftMax, height[l]);
            l++;
        } else {
            res += rightMax > height[r] ? rightMax - height[r] : 0;
            rightMax = Math.max(rightMax, height[r]);
            r--;
        }
    }

    return res;
}