题目描述

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

示例 1:

1
2
3

输入: coins = [1, 2, 5], amount = 11
输出: 3 
解释: 11 = 5 + 5 + 1

示例 2:

1 2	输入: coins = [2], amount = 3 输出: -1

说明:
你可以认为每种硬币的数量是无限的。

题解

动态规划

分析这道题的动态规划算法:

*确定 base case: * 很显然, 当金额为0的时候, 硬币组合数为0;

*确定状态: * 因为硬币的面额固定, 硬币数量无限, 为了保证子问题的相互独立性, 只能选取不同的金额作为状态.

*确定选择 : * 是什么能让状态不停地改变? 就是硬币的面额.

dp(n) 的定义：输入一个目标金额 n，返回凑出目标金额 n 的最少硬币数量。

状态转移方程为：

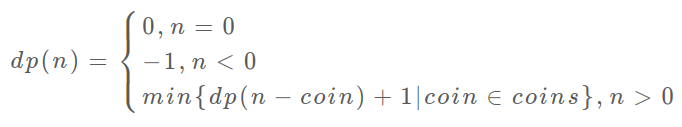
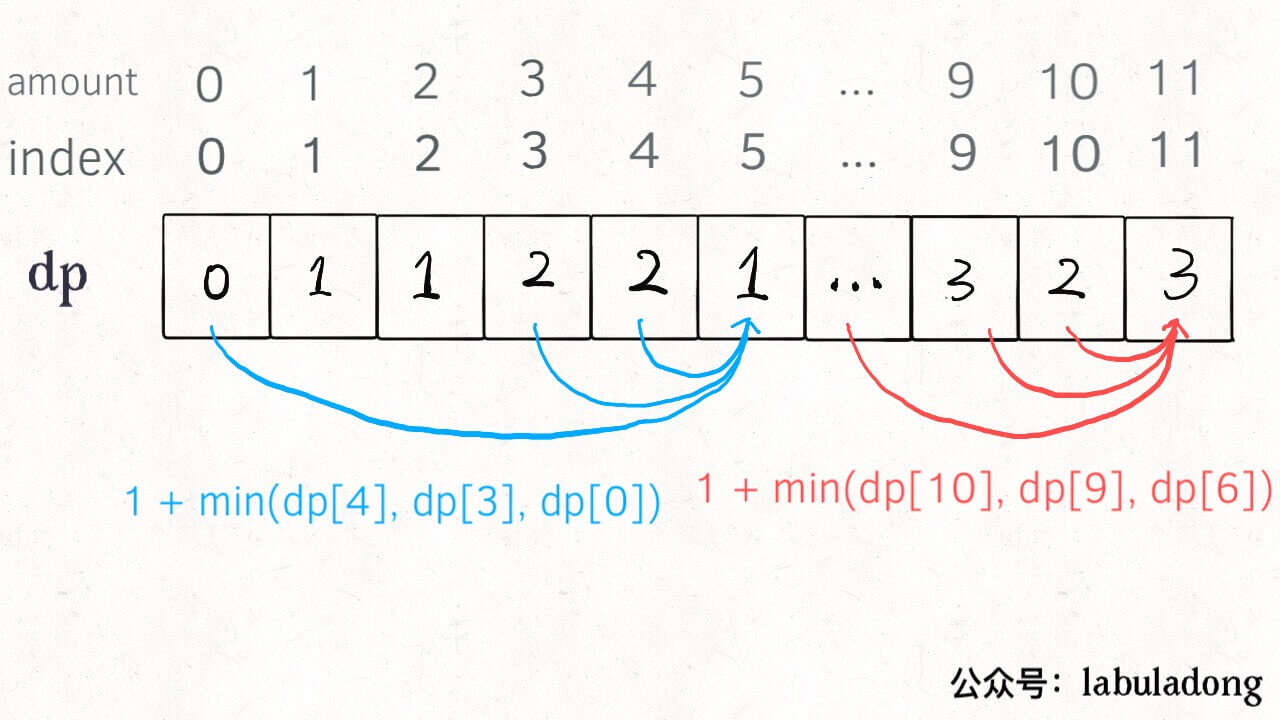
public int coinChange2(int[] coins, int amount) {
    int[] dp = new int[amount + 1];
    Arrays.fill(dp, amount + 1);
    dp[0] = 0;

    for (int i = 1; i < amount + 1; i++) {
        for (int coin : coins) {
            if (i - coin < 0)
                continue;
            dp[i] = Math.min(dp[i], 1 + dp[i - coin]);
        }
    }

    return dp[amount] == amount + 1 ? -1 : dp[amount];

}