题目描述

给定一个无序的整数数组，找到其中最长上升子序列的长度。

示例:

1
2
3

输入: [10,9,2,5,3,7,101,18]
输出: 4 
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

说明:

可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。

题解

动态规划

这是道典型的动态规划题目, 注意「子序列」和「子串」这两个名词的区别，子串一定是连续的，而子序列不一定是连续的。下面先来一步一步设计动态规划算法解决这个问题。

动态规划的核心设计思想是数学归纳法。

我们想证明一个数学结论，那么我们先假设这个结论在 k<n 时成立，然后想办法证明 k=n 的时候此结论也成立。如果能够证明出来，那么就说明这个结论对于 k 等于任何数都成立。

类似的，我们设计动态规划算法，不是需要一个 dp 数组吗？我们可以假设 dp[0…i−1] 都已经被算出来了，然后问自己：怎么通过这些结果算出dp[i] ?

我们的定义是这样的：dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度

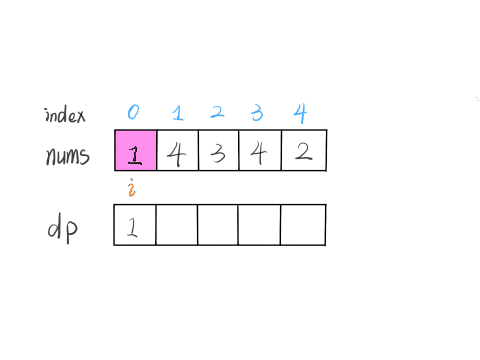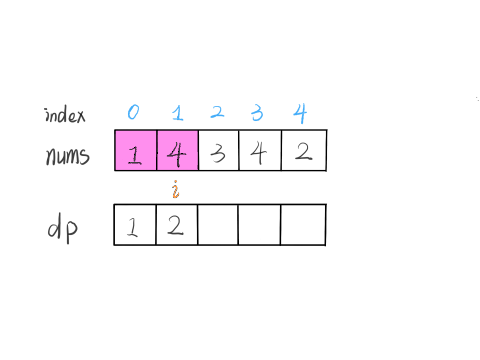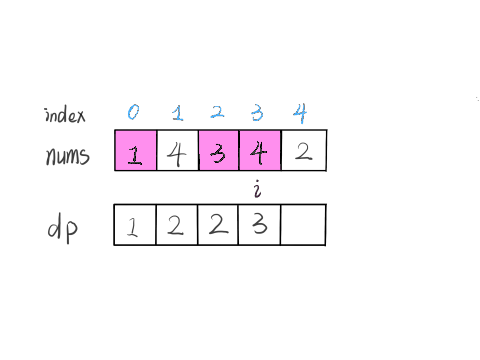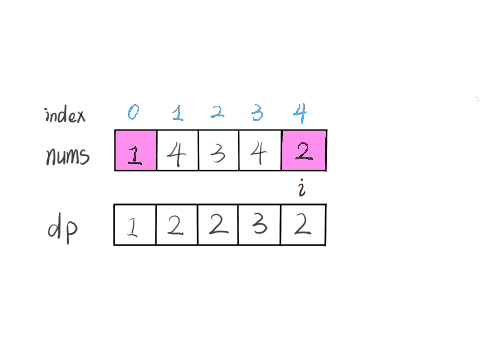
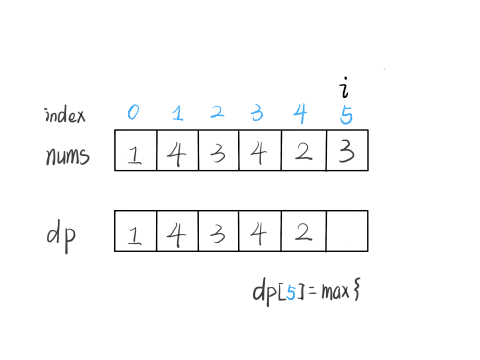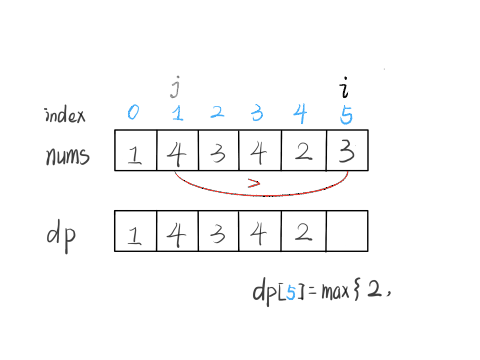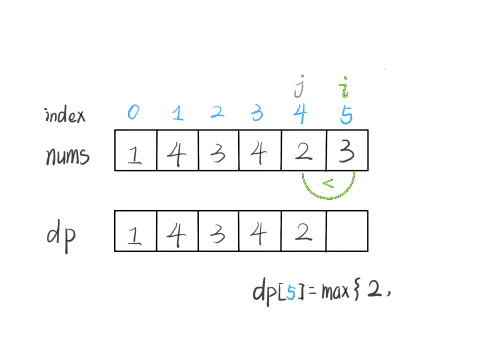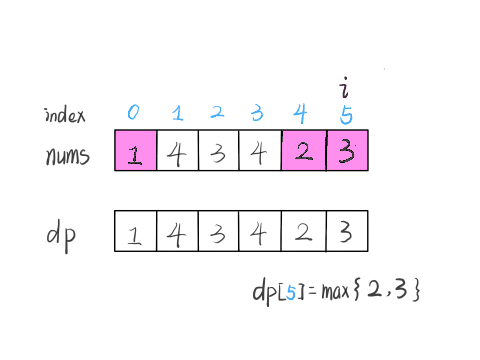
我们已经知道了 dp[0…4] 的所有结果，我们如何通过这些已知结果推出 dp[5] 呢？

根据刚才我们对 dp 数组的定义，现在想求 dp[5] 的值，也就是想求以 nums[5] 为结尾的最长递增子序列。

nums[5] = 3，既然是递增子序列，我们只要找到前面那些结尾比 3 小的子序列，然后把 3 接到最后，就可以形成一个新的递增子序列，而且这个新的子序列长度加一。

当然，可能形成很多种新的子序列，但是我们只要最长的，把最长子序列的长度作为 dp[5] 的值即可。

还有一个细节问题，就是 base case。dp 数组应该全部初始化为 1，因为子序列最少也要包含自己，所以长度最小为 1。

public int lengthOfLIS(int[] nums) {
    if (nums.length == 0)
        return 0;

    int res = 1;
    int[] dp = new int[nums.length];
    Arrays.fill(dp, 1);

    for (int i = 1; i < nums.length; i++) {
        for (int j = 0; j < i; j++) {
            if (nums[j] < nums[i]) {
                dp[i] = Math.max(dp[i], 1+dp[j]);
            }
        }
        res = Math.max(res, dp[i]);
    }
    return res;
}