72.编辑距离

发表于 | 分类于 | 本文总阅读量 次
字数统计: 1.6k | 阅读时长 ≈ 6

题目描述

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1：

1
2
3
4
5
6
输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

1
2
3
4
5
6
7
8
输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

题解

动态规划

一、思路

编辑距离问题就是给我们两个字符串s1和s2，只能用三种操作，让我们把s1变成s2，求最少的操作数。需要明确的是，不管是把s1变成s2还是反过来，结果都是一样的，所以后文就以s1变成s2举例。

解决两个字符串的动态规划问题，一般都是用两个指针i,j分别指向两个字符串的最后，然后一步步往前走，缩小问题的规模

设两个字符串分别为 “rad” 和 “apple”，为了把s1变成s2，算法会这样进行：

根据上面的 GIF，可以发现操作不只有三个，其实还有第四个操作，就是什么都不要做（skip）

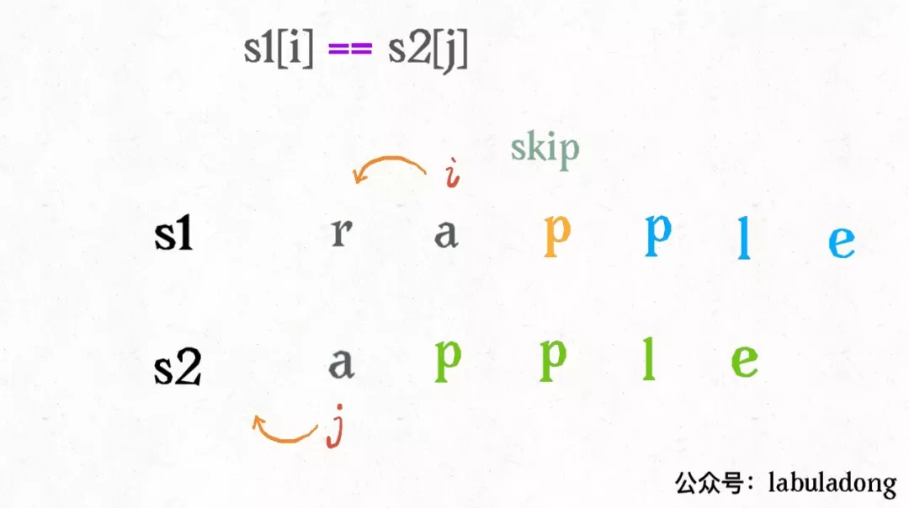
因为这两个字符本来就相同，为了使编辑距离最小，显然不应该对它们有任何操作，直接往前移动i,j即可。

还有一个很容易处理的情况，就是j走完s2时，如果i还没走完s1，那么只能用删除操作把s1缩短为s2。比如这个情况：

类似的，如果i走完s1时j还没走完了s2，那就只能用插入操作把s2剩下的字符全部插入s1。等会会看到，这两种情况就是算法的 base case。

二、代码详解

base case 是i走完s1或j走完s2，可以直接返回另一个字符串剩下的长度。

对于每对儿字符s1[i]和s2[j]，可以有四种操作：

1
2
3
4
5
6
7
8
if s1[i] == s2[j]:
    啥都别做（skip）
    i, j 同时向前移动
else:
    三选一：
        插入（insert）
        删除（delete）
        替换（replace）

有这个框架，问题就已经解决了。读者也许会问，这个「三选一」到底该怎么选择呢？很简单，全试一遍，哪个操作最后得到的编辑距离最小，就选谁。

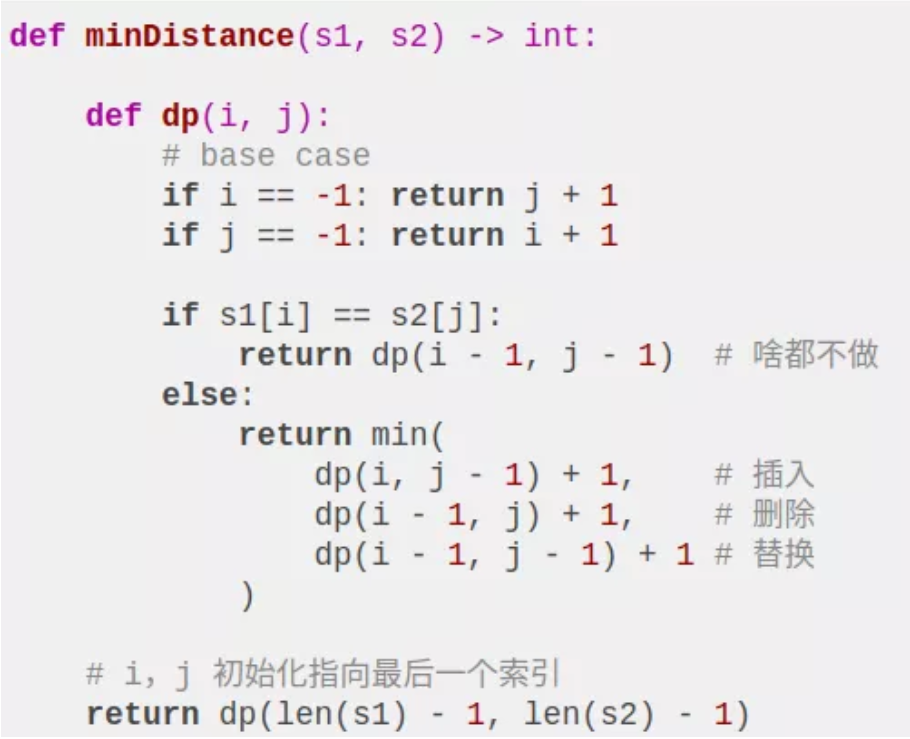
下面来详细解释一下这段递归代码，base case 应该不用解释了，主要解释一下递归部分。

都说递归代码的可解释性很好，这是有道理的，只要理解函数的定义，就能很清楚地理解算法的逻辑。我们这里 dp(i, j) 函数的定义是这样的：

1
2
def dp(i, j) -> int
# 返回 s1[0..i] 和 s2[0..j] 的最小编辑距离

记住这个定义之后，先来看这段代码：

1
2
3
4
5
6
7
if s1[i] == s2[j]:
    return dp(i - 1, j - 1)  # 啥都不做
# 解释：
# 本来就相等，不需要任何操作
# s1[0..i] 和 s2[0..j] 的最小编辑距离等于
# s1[0..i-1] 和 s2[0..j-1] 的最小编辑距离
# 也就是说 dp(i, j) 等于 dp(i-1, j-1)

如果s1[i]！=s2[j]，就要对三个操作递归了，稍微需要点思考：

1
2
3
4
5
dp(i, j - 1) + 1,    # 插入
# 解释：
# 我直接在 s1[i] 插入一个和 s2[j] 一样的字符
# 那么 s2[j] 就被匹配了，前移 j，继续跟 i 对比
# 别忘了操作数加一

1
2
3
4
5
dp(i - 1, j) + 1,  # 删除
\# 解释：
\# 我直接把 s[i] 这个字符删掉
\# 前移 i，继续跟 j 对比
\# 操作数加一

1
2
3
4
5
dp(i - 1, j - 1) + 1 # 替换
\# 解释：
\# 我直接把 s1[i] 替换成 s2[j]，这样它俩就匹配了
\# 同时前移 i，j 继续对比
\# 操作数加一

现在，你应该完全理解这段短小精悍的代码了。还有点小问题就是，这个解法是暴力解法，存在重叠子问题，需要用动态规划技巧来优化。

怎么能一眼看出存在重叠子问题呢？前文 动态规划之正则表达式 有提过，这里再简单提一下，需要抽象出本文算法的递归框架：

1
2
3
4
def dp(i, j):
    dp(i - 1, j - 1) #1
    dp(i, j - 1)     #2
    dp(i - 1, j)     #3

对于子问题dp(i-1,j-1)，如何通过原问题dp(i,j)得到呢？有不止一条路径，比如dp(i,j)->#1和dp(i,j)->#2->#3。一旦发现一条重复路径，就说明存在巨量重复路径，也就是重叠子问题。

三、动态规划优化

首先明确 dp 数组的含义，dp 数组是一个二维数组，长这样：

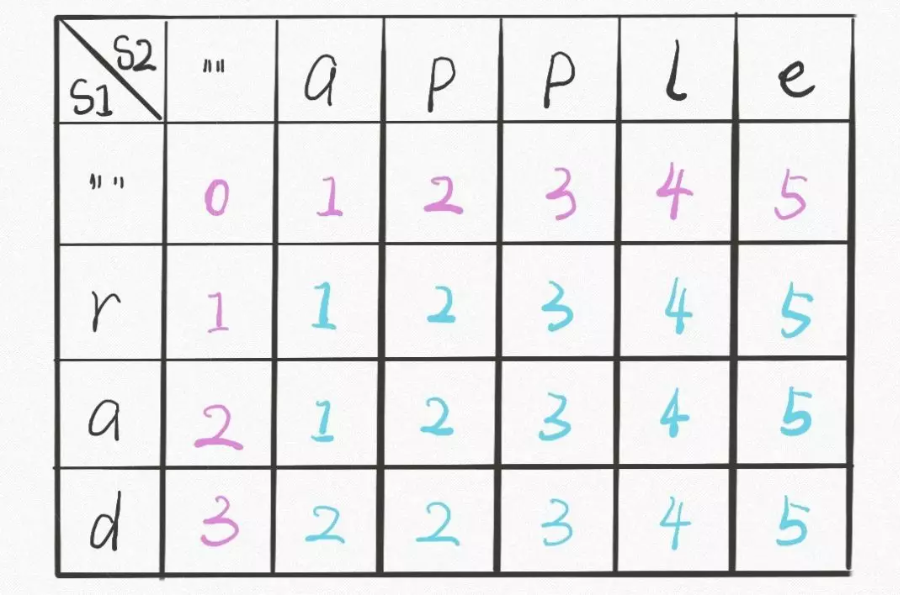
dp[i][j]的含义和之前的 dp 函数类似：

1
2
3
4
5
def dp(i, j) -> int
# 返回 s1[0..i] 和 s2[0..j] 的最小编辑距离

dp[i-1][j-1]
# 存储 s1[0..i] 和 s2[0..j] 的最小编辑距离

有了之前递归解法的铺垫，应该很容易理解。dp 函数的 base case 是i,j等于 -1，而数组索引至少是 0，所以 dp 数组会偏移一位，dp[..][0]和dp[0][..]对应 base case。。

既然 dp 数组和递归 dp 函数含义一样，也就可以直接套用之前的思路写代码，唯一不同的是，DP table 是自底向上求解，递归解法是自顶向下求解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class lc72 {
    public int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length();
        int[][] dp = new int[m + 1][n + 1];

        for (int i = 0; i <= m; i++) {
            dp[i][0] = i;
        }

        for (int j = 0; j <= n; j++) {
            dp[0][j] = j;
        }

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (word1.charAt(m - 1) == word2.charAt(n - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = min( dp[i - 1][j] + 1,
                                    dp[i][j - 1] + 1,
                                    dp[i - 1][j - 1] + 1
                    );
                }
            }
        }

        return dp[m][n];

    }

    private int min(int x, int y, int z) {
        return Math.min(x, Math.min(y, z));
    }

}
-------------本文结束感谢您的阅读-------------
可以请我喝杯奶茶吗