题目描述

你将获得 K 个鸡蛋，并可以使用一栋从 1 到 N 共有 N 层楼的建筑。

每个蛋的功能都是一样的，如果一个蛋碎了，你就不能再把它掉下去。

你知道存在楼层 F ，满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎，从 F 楼层或比它低的楼层落下的鸡蛋都不会破。

每次移动，你可以取一个鸡蛋（如果你有完整的鸡蛋）并把它从任一楼层 X 扔下（满足 1 <= X <= N）。

你的目标是确切地知道 F 的值是多少。

无论 F 的初始值如何，你确定 F 的值的最小移动次数是多少？

示例 1：

输入：K = 1, N = 2
输出：2
解释：
鸡蛋从 1 楼掉落。如果它碎了，我们肯定知道 F = 0 。
否则，鸡蛋从 2 楼掉落。如果它碎了，我们肯定知道 F = 1 。
如果它没碎，那么我们肯定知道 F = 2 。
因此，在最坏的情况下我们需要移动 2 次以确定 F 是多少。

示例 2：

1 2	输入：K = 2, N = 6 输出：3

示例 3：

1 2	输入：K = 3, N = 14 输出：4

题解

动态规划+二分查找

关于解题的思路, 李永乐老师讲的非常详细且清晰, 见视频:

李永乐老师双蛋问题视频

如果鸡蛋不碎，那么状态变成 (K, N-X)，即我们鸡蛋的数目不变，但答案只可能在上方的 N-X层楼了。也就是说，我们把原问题缩小成了一个规模为 (K, N-X) 的子问题；

如果鸡蛋碎了，那么状态变成 (K-1, X-1)，即我们少了一个鸡蛋，但我们知道答案只可能在第 XX 楼下方的 X-1X−1 层楼中了。也就是说，我们把原问题缩小成了一个规模为 (K-1, X-1)的子问题。

这样一来，我们定义 dp(K, N)为在状态 (K, N) 下最少需要的步数。根据以上分析我们可以列出状态转移方程：

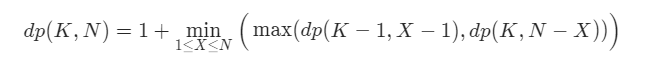
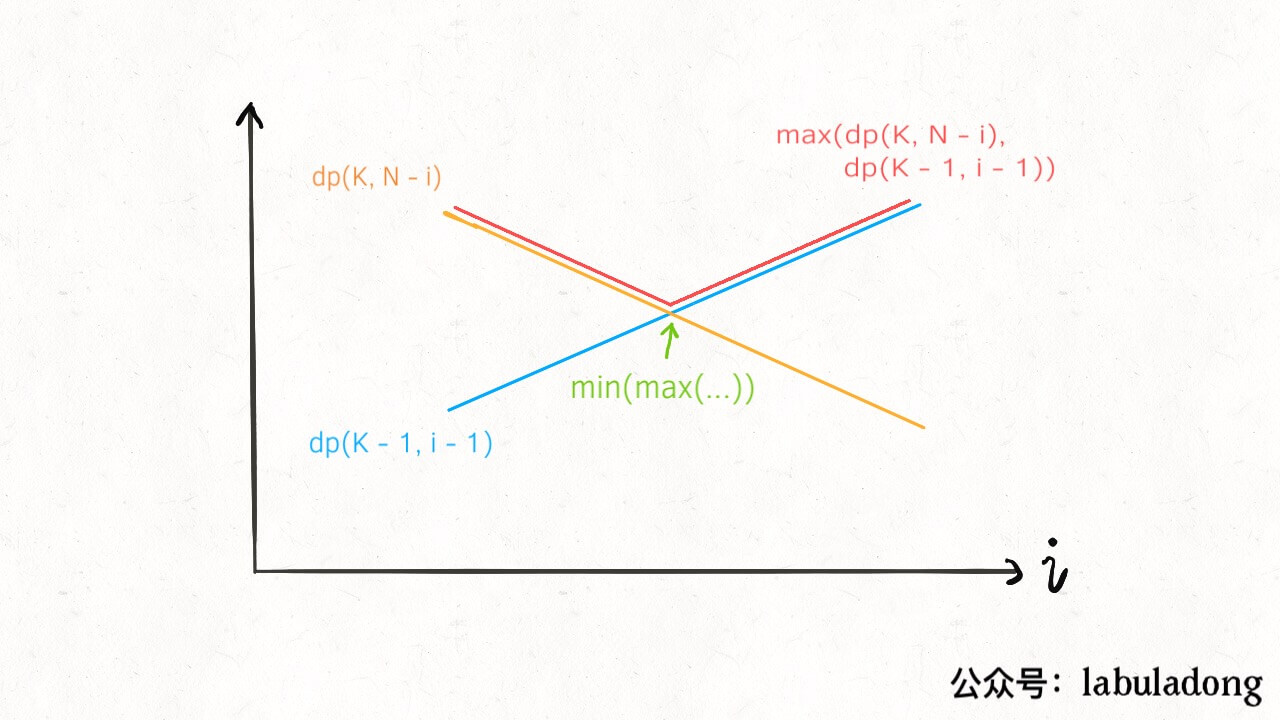
首先我们根据 dp(K, N) 数组的定义（有 K 个鸡蛋面对 N 层楼，最少需要扔几次），很容易知道 K 固定时，这个函数随着 N 的增加一定是单调递增的，无论你策略多聪明，楼层增加测试次数一定要增加。

那么注意 dp(K - 1, i - 1) 和 dp(K, N - i) 这两个函数，其中 i 是从 1 到 N 单增的，如果我们固定 K 和 N，把这两个函数看做关于 i 的函数，前者随着 i 的增加应该也是单调递增的，而后者随着 i 的增加应该是单调递减的：

public int superEggDrop(int K, int N) {

    int[][] dp = new int[N + 1][K + 1];

    for (int i = 1; i <= N; i++) {
        Arrays.fill(dp[i], i);
    }

    for (int i = 1; i <= N; i++) {
        dp[i][0] = 0;
    }

    for (int i = 2; i <= N; i++) {
        for (int j = 2; j <= K; j++) {
            // 在区间 [1, i] 里确定一个最优值
            int left = 1;
            int right = i;
            while (left < right) {
                // 找 dp[k - 1][j - 1] <= dp[i - mid][j] 的最大值 k
                int mid = left + (right - left + 1) / 2;

                int breakCount = dp[mid - 1][j - 1];
                int notBreakCount = dp[i - mid][j];
                if (breakCount > notBreakCount) {
                    // 排除法（减治思想）写对二分见第 35 题，先想什么时候不是解
                    // 严格大于的时候一定不是解，此时 mid 一定不是解
                    // 下一轮搜索区间是 [left, mid - 1]
                    right = mid - 1;
                } else {
                    // 这个区间一定是上一个区间的反面，即 [mid, right]
                    // 注意这个时候取中间数要上取整，int mid = left + (right - left + 1) / 2;
                    left = mid;
                }
            }
            // left 这个下标就是最优的 k 值，把它代入转移方程 Math.max(dp[k - 1][j - 1], dp[i - k][j]) + 1) 即可
            dp[i][j] = Math.max(dp[left - 1][j - 1], dp[i - left][j]) + 1;

        }
    }

    return dp[N][K];
}