题目描述

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

示例 1：

1
2
3

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:

1
2
3

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

题解

数学推导

推导过程见连接

直接给结论:

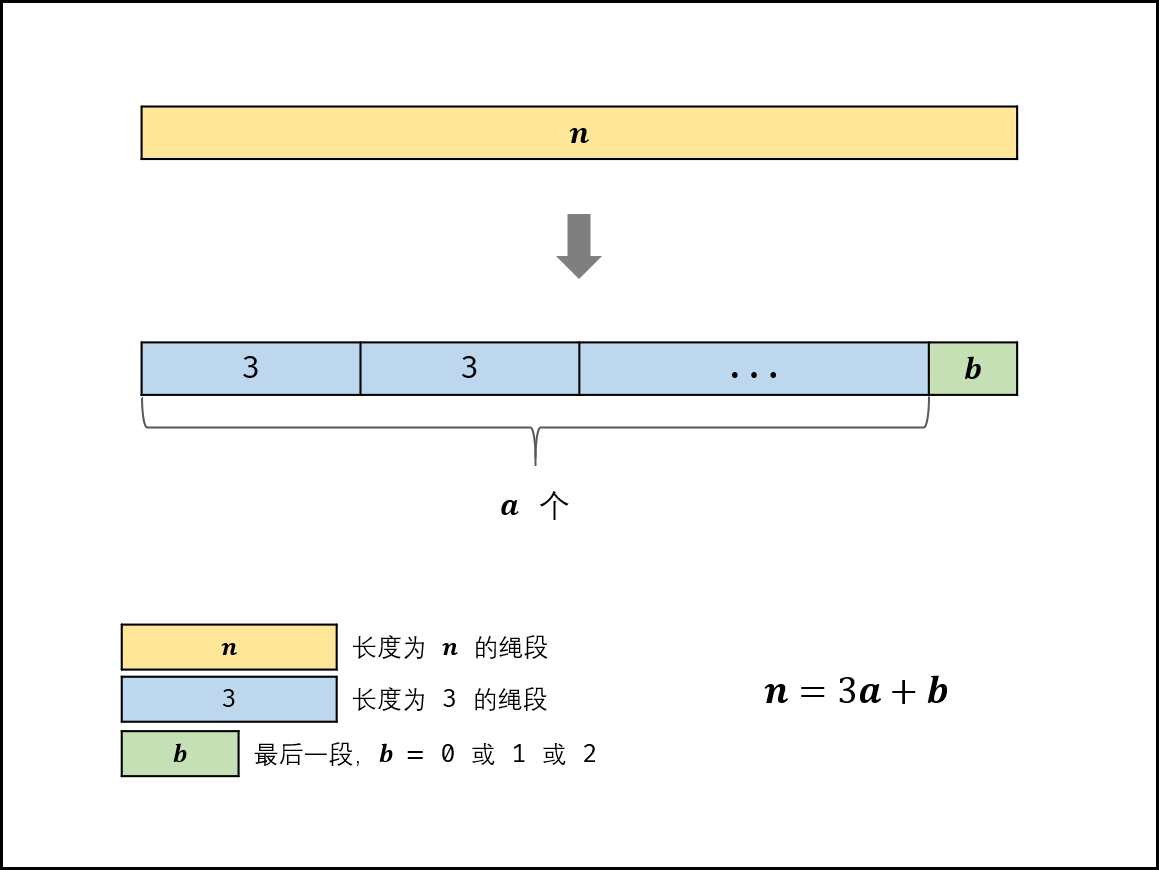
切分规则：

最优： 3 。把绳子尽可能切为多个长度为 3 的片段，留下的最后一段绳子的长度可能为 0,1,2 三种情况。

次优： 2 。若最后一段绳子长度为 2 ；则保留，不再拆为 1+1 。

最差： 1 。若最后一段绳子长度为 1 ；则应把一份 3 + 1 替换为 2 + 2,

public int cuttingRope(int n) {
    if (n <= 3) return n - 1;
    int a = n / 3;
    int b = n % 3;
    if (b == 0) return (int) Math.pow(3, a);
    if (b == 1) return (int) (Math.pow(3, a - 1) * 4);
    return (int) (Math.pow(3, a) * 2);
}

暴力递归 + 备忘录(自顶向下)

设 F(n) 为长度为 n 的绳子可以得到的最大乘积，对于每一个 F(n)，可以得到如下分解：

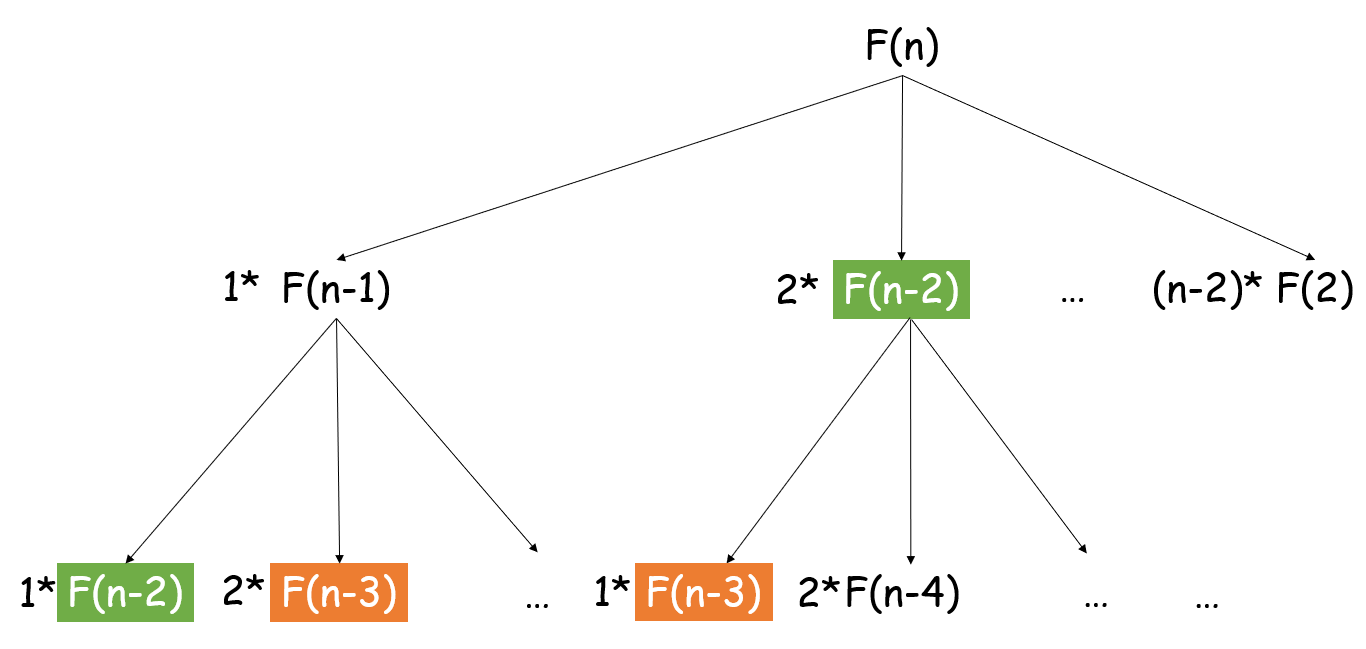
分治思想的解决方法往往是递归，注意到我们每次将一段绳子剪成两段时，剩下的部分可以继续剪，也可以不剪，因此我们得到了递归函数

HashMap<Integer, Integer> map = new HashMap<>();

public int cuttingRope2(int n) {
    if (n == 2)
        return 1;

    int res = Integer.MIN_VALUE;
    if (map.containsKey(n))
        return map.get(n);

    for (int i = 1; i <= n - 2; i++) {
        res = Math.max(res, Math.max(i * cuttingRope2(n - i), i * (n - i)));
    }

    map.put(n, res);

    return map.get(n);
}

动态规划(自底向上)

其实就是把上面的备忘录改为DP Table的形式, 编程顺序改为自底向上

public int cuttingRope3(int n) {
    if (n == 2) return 1;

    int[] dp = new int[n + 1];

    dp[1] = 1;
    dp[2] = 1;
    for (int i = 3; i <= n; i++) {
        for (int j = 1; j<=i-2;j++){
            dp[i] = Math.max(dp[i], Math.max(j*dp[i-j], j*(i-j)));
        }
    }
    return dp[n];
}