题目描述

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

示例 1:

输入: 
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物

题解

DFS递归

在棋盘中任意一格的位置, 都有两个方向可以选择, 一个是向下, 一个是向右, 采用先序遍历的方式, 在两个方向中选择价值更高的去走. 而终止条件有两种, 一种是走到了右下角, 即grid[m-1][n-1] 的位置, 另外一种是越界, 直接返回一个Integer.MIN_VALUE

int m;
int n;
int[][] grid;

public int maxValue(int[][] grid) {
    this.m = grid.length;
    this.n = grid[0].length;
    this.grid = grid;
    return pathSum(0, 0);
}

private int pathSum(int i, int j) {
    if (i == m - 1 && j == n - 1) {
        return grid[i][j];
    }
    if (i == m || j == n)
        return Integer.MIN_VALUE;
    return grid[i][j] + Math.max(pathSum(i + 1, j), pathSum(i, j + 1));
}

动态规划

与递归的思路一样, 但是方向相反, 动态规划的状态dp[i][j] 表示走到棋盘grid[i][j]位置处的最大价值.

因为只能往右边和下边走, 那么每个位置的最大价值为上方和左方中的较大价值加上本格的价值, 即状态转移方程是:

1	dp[i][j] = grid[i][j] + Math.max(dp[i-1][j], dp[i][j-1]);

base case 的情况比较容易理解, 就是从起点开始一路向下或者一路向右通过累加的方式就可以直接算出来

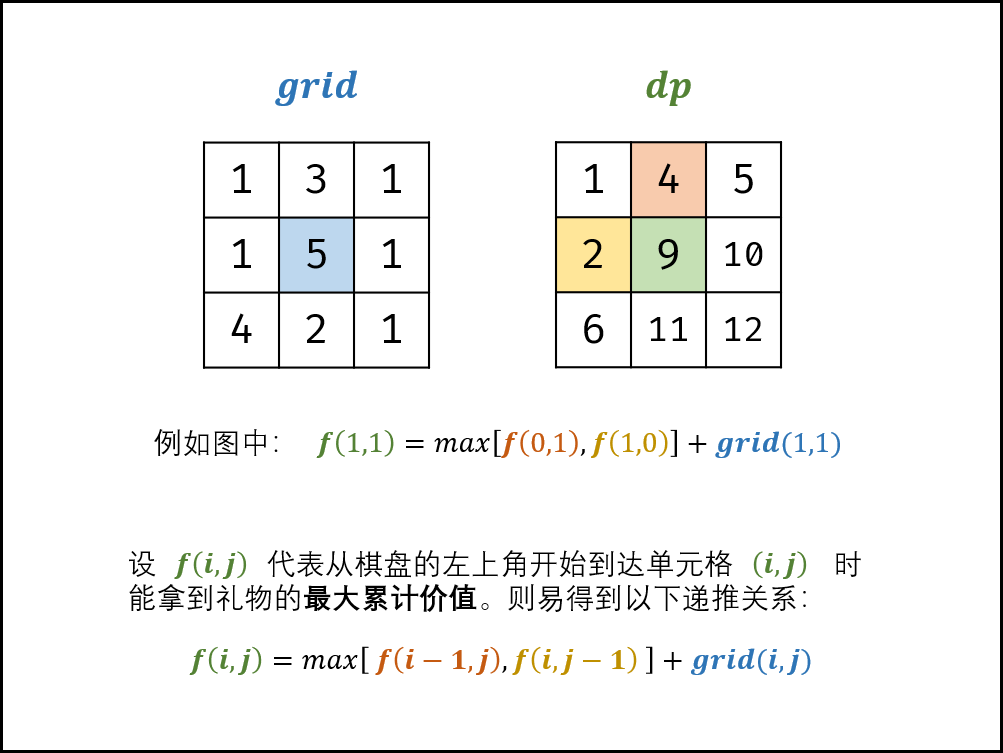
public int maxValue2(int[][] grid) {
    int m = grid.length;
    int n = grid[0].length;

    int[][] dp = new int[m][n];
    dp[0][0] = grid[0][0];

    for (int i = 1; i < m; i++) {
        dp[i][0] = dp[i - 1][0] + grid[i][0];
    }

    for (int j = 1; j < n; j++) {
        dp[0][j] = dp[0][j - 1] + grid[0][j];
    }

    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = grid[i][j] + Math.max(dp[i - 1][j], dp[i][j - 1]);
        }
    }

    return dp[m-1][n-1];
}