题目描述

假设把某股票的价格按照时间先后顺序存储在数组中，请问买卖该股票一次可能获得的最大利润是多少？

示例 1:

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

示例 2:

1
2
3

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

题解

迭代

思路是遍历每个数值, 以该数值为起点, 遍历后面的所有价格, 也就是算出从每个价格买入的话利润为多少, 取最大的值

public int maxProfit(int[] prices) {

    int res = 0;

    for (int i = 0; i < prices.length - 1; i++) {
        for (int j = i + 1; j < prices.length; j++) {
            if (prices[j] > prices[i]) {
                res = Math.max(res, prices[j] - prices[i]);
            }
        }
    }

    return res;
}

动态规划

采用动态规划的思想,令dp[i] 表示以prices[i]结尾时的最大利润为多少.

每个状态与它之前的状态是有转换关系的

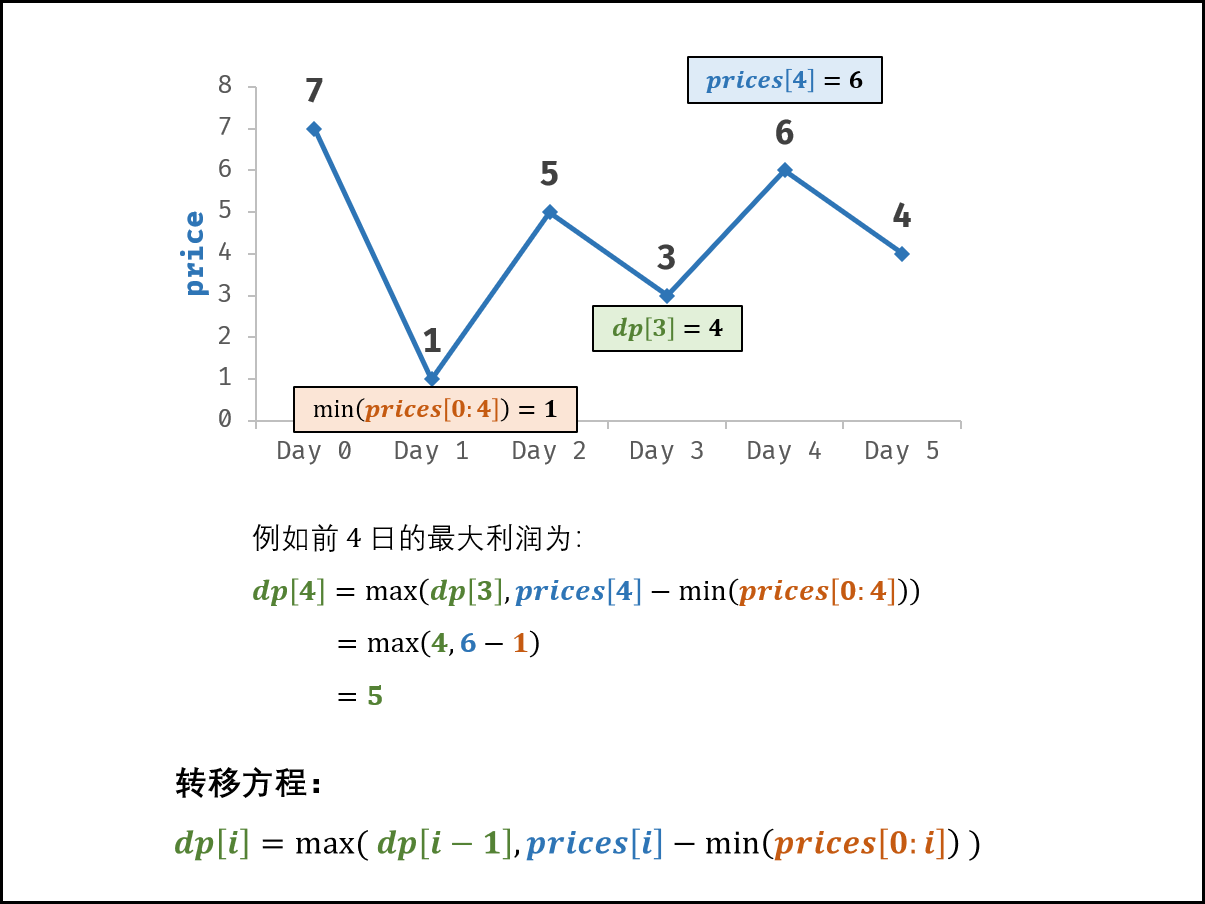
使用这种方法只需要创建一个整型变量记录最小的值即可.

public int maxProfit2(int[] prices) {
    if (prices.length==0)
        return 0;

    int[] dp = new int[prices.length];
    int min = Integer.MAX_VALUE;
    dp[0] = 0;


    for (int i = 1; i < prices.length; i++) {
        min = Math.min(min, prices[i]);
        dp[i] = Math.max(dp[i - 1], prices[i] - min);

    }
    return dp[prices.length - 1];
}

动态规划简化后的代码

public int maxProfit(int[] prices) {
    int min = Integer.MAX_VALUE;
    int res = 0;

    for(int price: prices){
        min = Math.min(price, min);
        res = Math.max(res, price-min);
    }
    return res;
}

另一种动态规划思路

为了与其他的股票问题建立思路上的联系, 考虑这样的一种动态规划思路:

状态

DP table 用二维数组来表示: *dp[i] [j] *表示第i天在不同状态下的最大利润. 其中i是表示天数, j表示持有股票的状态, j只有0或1两种可能. 其中0表示不持有股票, 1表示持有股票

状态转移方程

dp[i][0]: 表示第i天不持股, 那么可能是第i-1天也不持股保持下来的, 也可能是把第i-1 天的股票卖出所以不持股,得出转移方程为

1	dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])

dp[i][1]: 表示第i天持股, 那么可能是第i-1天就持股保持下来的, 也可能是之前不持股第i天买入的, 得出转移方程为:

1	dp[i][1] = max(dp[i-1][1], -prices[i])

需要注意的是, 因为只允许一次交易, 所以不能加上dp[i-1][0]

初始值

第0天不持股, dp[0][0]=0

第0天持股, dp[0][1]=-prices[i]

输出
dp[len-1][0]

public int maxProfit(int[] prices) {
    int len = prices.length;
    if (len < 2) {
        return 0;
    }

    int[][] dp = new int[len][2];
    dp[0][0] = 0;
    dp[0][1] = -prices[0];

    for (int i = 1; i < len; i++) {
        dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]+prices[i]);
        dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
    }

    return dp[len-1][0];
}