题目描述

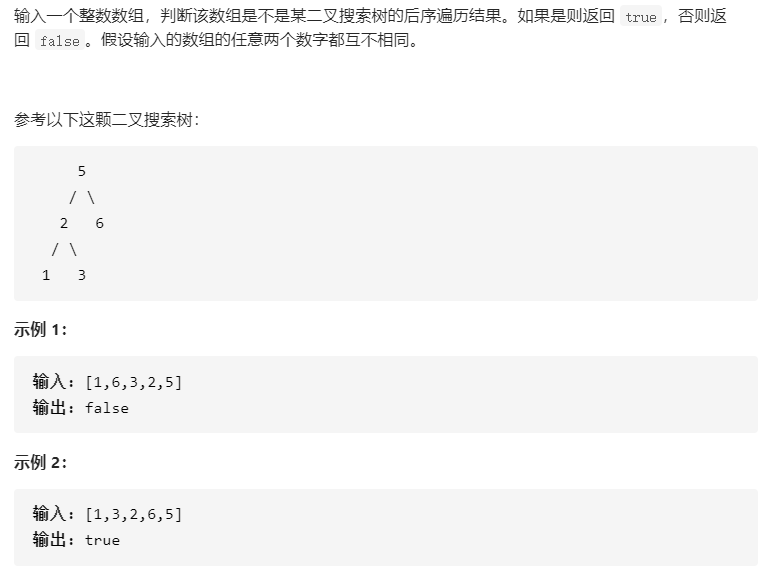
题解

分治递归

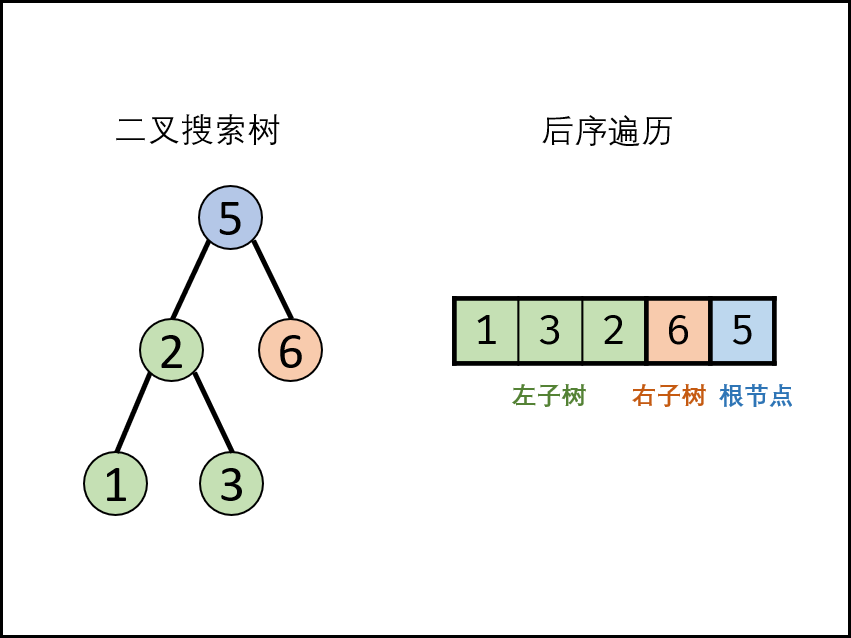
后序遍历定义： [ 左子树 | 右子树 | 根节点 ] ，即遍历顺序为 “左、右、根” 。

二叉搜索树定义： 左子树中所有节点的值 << 根节点的值；右子树中所有节点的值 >> 根节点的值；其左、右子树也分别为二叉搜索树。

终止条件： 当 i \geq ji≥j ，说明此子树节点数量 \leq 1≤1 ，无需判别正确性，因此直接返回 truetru**e ；

递推工作：

首先划分左右子树, 划分的标准是, 从该序列头部开始遍历, 遍历到第一个大于根节点的位置m, 则刚才遍历的所有元素都属于左子树
从m位置开始的所有元素都要比根节点的数值大才能说明该后序遍历数组合法

public boolean verifyPostorder(int[] postorder) {
    return recur(postorder, 0, postorder.length - 1);
}

private boolean recur(int[] postorder, int i, int j) {
    if (i >= j) {
        return true;
    }

    int p = i;
    while (postorder[p] < postorder[j]) {
        p++;
    }
    int m = p;
    while (postorder[p] > postorder[j]) {
        p++;
    }
    return p == j && recur(postorder, i, m - 1) && recur(postorder, m, j - 1);

}