题目描述

亚历克斯和李用几堆石子在做游戏。偶数堆石子排成一行，每堆都有正整数颗石子 piles[i] 。

游戏以谁手中的石子最多来决出胜负。石子的总数是奇数，所以没有平局。

亚历克斯和李轮流进行，亚历克斯先开始。每回合，玩家从行的开始或结束处取走整堆石头。这种情况一直持续到没有更多的石子堆为止，此时手中石子最多的玩家获胜。

假设亚历克斯和李都发挥出最佳水平，当亚历克斯赢得比赛时返回 true ，当李赢得比赛时返回 false 。

示例：

输入：[5,3,4,5]
输出：true
解释：
亚历克斯先开始，只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗，这一行就变成了 [3,4,5] 。
如果李拿走前 3 颗，那么剩下的是 [4,5]，亚历克斯拿走后 5 颗赢得 10 分。
如果李拿走后 5 颗，那么剩下的是 [3,4]，亚历克斯拿走后 4 颗赢得 9 分。
这表明，取前 5 颗石子对亚历克斯来说是一个胜利的举动，所以我们返回 true 。

2 <= piles.length <= 500
piles.length 是偶数。
1 <= piles[i] <= 500
sum(piles) 是奇数。

题解

动态规划

介绍 dp 数组的含义之前，我们先看一下 dp 数组最终的样子：

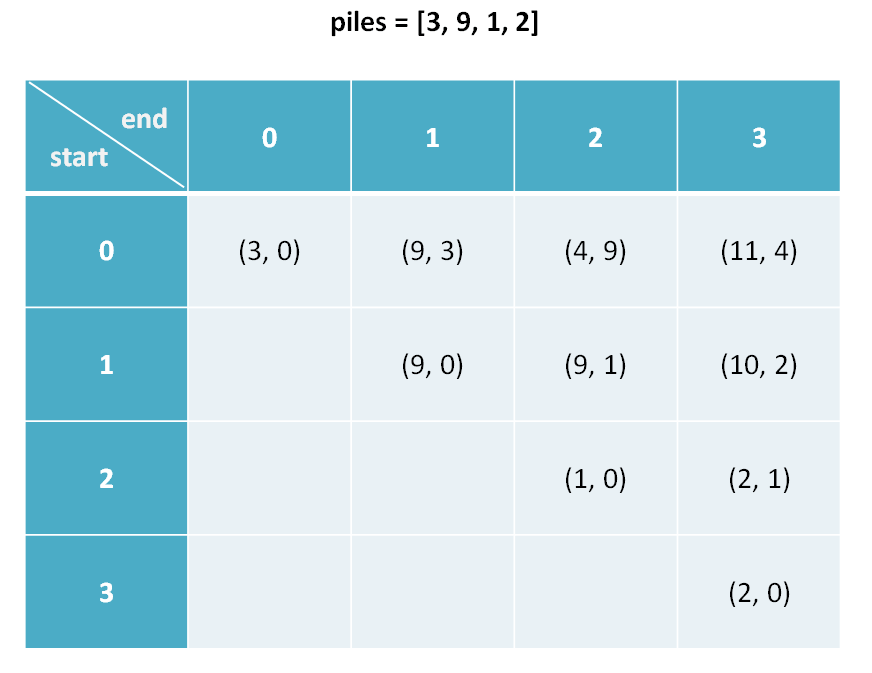
以下是对 dp 数组含义的解释：

dp[i][j].fir 表示，对于 piles[i...j] 这部分石头堆，先手能获得的最高分数。
dp[i][j].sec 表示，对于 piles[i...j] 这部分石头堆，后手能获得的最高分数。

举例理解一下，假设 piles = [3, 9, 1, 2]，索引从 0 开始
dp[0][1].fir = 9 意味着：面对石头堆 [3, 9]，先手最终能够获得 9 分。
dp[1][3].sec = 2 意味着：面对石头堆 [9, 1, 2]，后手最终能够获得 2 分。

写状态转移方程很简单，首先要找到所有「状态」和每个状态可以做的「选择」，然后择优。

根据前面对 dp 数组的定义，状态显然有三个：开始的索引 i，结束的索引 j，当前轮到的人。

对于这个问题的每个状态，可以做的选择有两个：选择最左边的那堆石头，或者选择最右边的那堆石头。 我们可以这样穷举所有状态：

n = piles.length
for 0 <= i < n:
    for j <= i < n:
        for who in {fir, sec}:
            dp[i][j][who] = max(left, right)

这道题的难点在于，两人是交替进行选择的，也就是说先手的选择会对后手有影响，这怎么表达出来呢？

根据我们对 dp 数组的定义，很容易解决这个难点，写出状态转移方程：

dp[i][j].fir = max(piles[i] + dp[i+1][j].sec, piles[j] + dp[i][j-1].sec)
dp[i][j].fir = max(    选择最左边的石头堆     ,     选择最右边的石头堆     )
# 解释：我作为先手，面对 piles[i...j] 时，有两种选择：
# 要么我选择最左边的那一堆石头，然后面对 piles[i+1...j]
# 但是此时轮到对方，相当于我变成了后手；
# 要么我选择最右边的那一堆石头，然后面对 piles[i...j-1]
# 但是此时轮到对方，相当于我变成了后手。

if 先手选择左边:
    dp[i][j].sec = dp[i+1][j].fir
if 先手选择右边:
    dp[i][j].sec = dp[i][j-1].fir
# 解释：我作为后手，要等先手先选择，有两种情况：
# 如果先手选择了最左边那堆，给我剩下了 piles[i+1...j]
# 此时轮到我，我变成了先手；
# 如果先手选择了最右边那堆，给我剩下了 piles[i...j-1]
# 此时轮到我，我变成了先手

根据 dp 数组的定义，我们也可以找出 base case，也就是最简单的情况

dp[i][j].fir = piles[i]
dp[i][j].sec = 0
其中 0 <= i == j < n
# 解释：i 和 j 相等就是说面前只有一堆石头 piles[i]
# 那么显然先手的得分为 piles[i]
# 后手没有石头拿了，得分为 0

这里需要注意一点，我们发现 base case 是斜着的，而且我们推算 dp[i][j] 时需要用到 dp[i+1][j]和dp[i][j-1]:

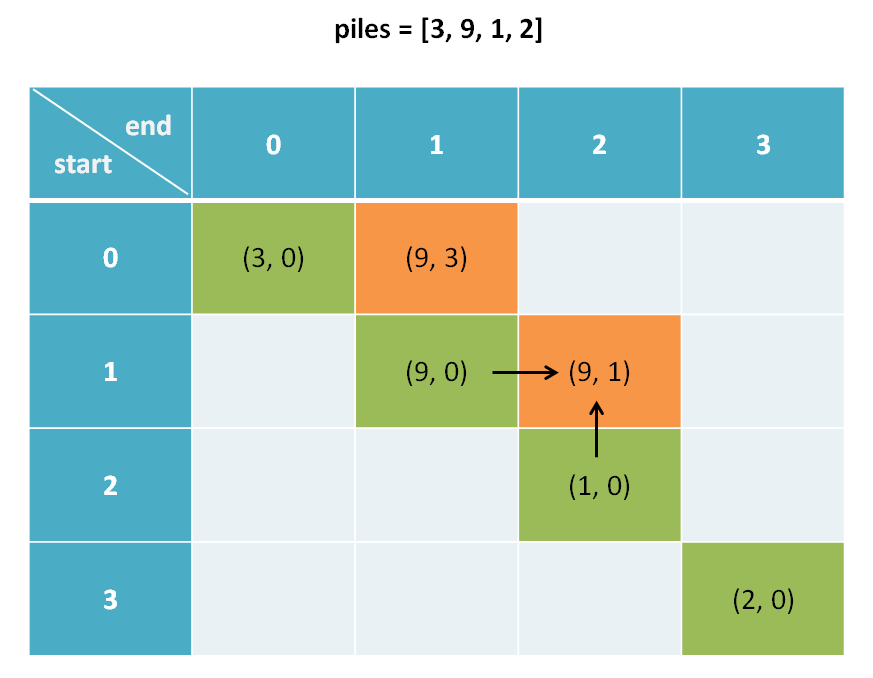
所以说算法不能简单的一行一行遍历 dp 数组，而要斜着遍历数组：

class Couple {
    int fir;
    int sec;

    public Couple() {
    }

    public Couple(int fir, int sec) {
        this.fir = fir;
        this.sec = sec;
    }
}

public boolean stoneGame(int[] piles) {
    int len = piles.length;

    Couple[][] dp = new Couple[len][len];

    for (int i = 0; i < len; i++) {
        dp[i][i] = new Couple(piles[i], 0);
    }

    for (int l = 1; l < len; l++) {
        for (int j = l; j < len; j++) {
            int i = j - l;

            dp[i][j] = new Couple(0, 0);
            int left = piles[i] + dp[i + 1][j].sec;
            int right = piles[j] + dp[i][j - 1].sec;
            if (left > right) {
                dp[i][j].fir = left;
                dp[i][j].sec = dp[i + 1][j].fir;
            } else {
                dp[i][j].fir = right;
                dp[i][j].sec = dp[i][j - 1].fir;
            }
        }
    }

    return dp[0][len - 1].fir > dp[0][len - 1].sec;

}

为了降低时间和空间复杂度, 可以不定义一个类来表示先手和后手一对元素, 而是采用三维数组的方式:

1 2	dp[i][j][0]表示先手获得的总数 dp[i][j][1]表示后手获得的总数